This page was generated from `/home/lectures/exp3/source/notebooks/L11/Diffraction Grating.ipynb`_.
Diffraction Grating¶
We would like to combine now the diffraction on individual slits with the multiple inteference from many slits. Such objects are called diffraction gratings and have large importance for spectroscopy but also for the compression of short laser pulses.
Let’s have a look at the sketch below.
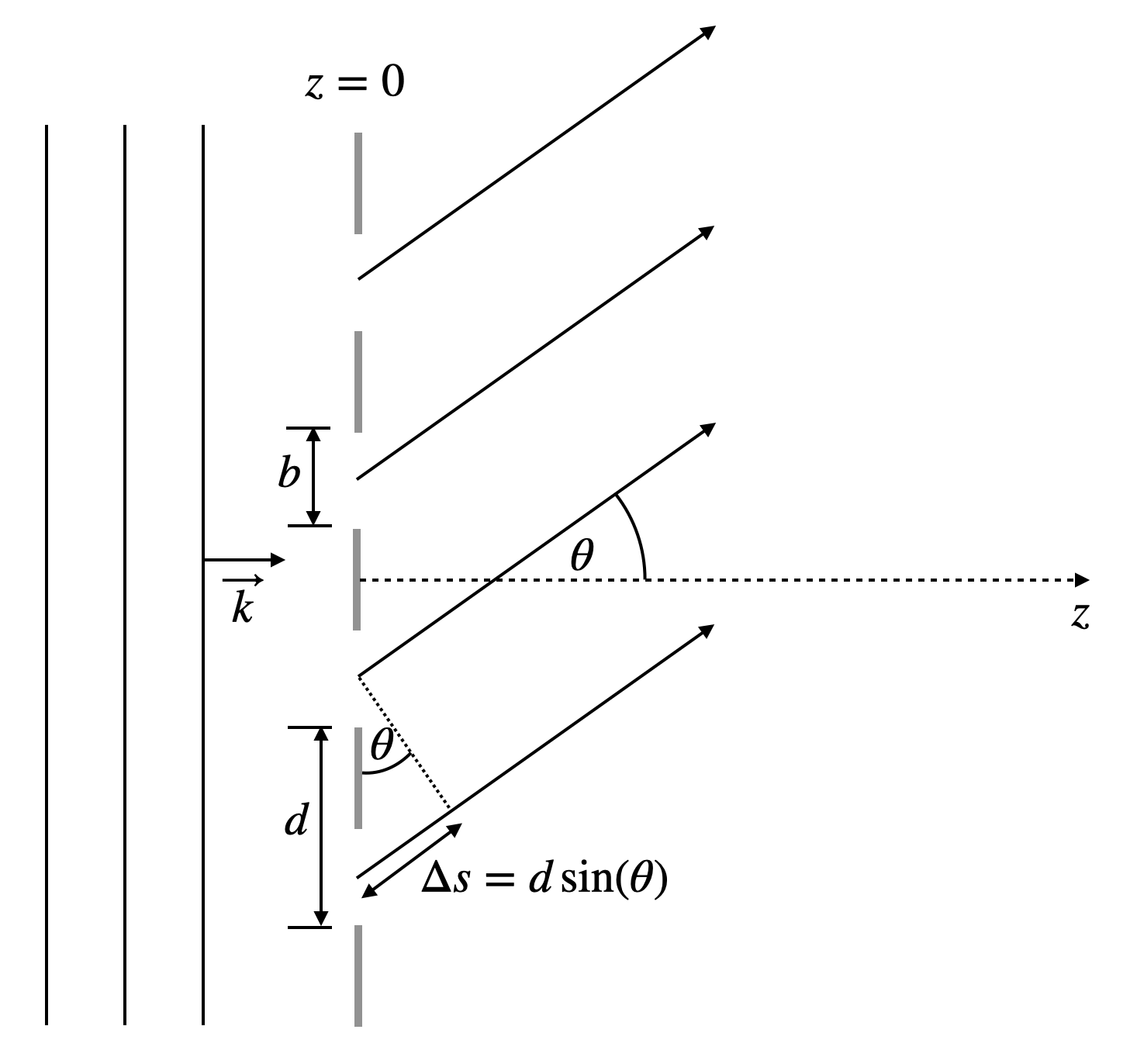
Fig.:
We consider a number of
Now we have multiple of these “slit” sources. Each Huygens source in a slit has a corresponding Huygens source in a neighboring slit at a distance
where the phase difference between neighboring waves is given by
which finally gives
The intensity distribution behind a diffraction grating is now given as the product of the two contributions of single slit diffraction and multiple source interference.
Diffraction Grating
The intensity distribution generated by a diffraction grating from monochromatic light and observed in the far field is given by
where
Properties of the diffraction pattern¶
We may now have a look at the properties of this intensity distribution. The graph below plots the intensity distribution for a diffraction grating with
The intensity pattern is consisting as we already calculated for the multiple wave interference. The main maxima are called diffraction orders charachetrized by an integer number. The central peak is the 0th order peak. The first main peak to the right is 1st diffraction order and so on.
The main peaks are seperated by
The intensity distribution is characterized by an envelope, which is the diffraction pattern of a single slit (dashed line). Thus in the example below the 2nd order peak is suppressed. The envelope will become wider, if the slits become narrower.
Position of the Main Peaks¶
The position of the main peaks requires that the numerator and the denominator are zero. This is given whenever the denominator argument is a integer multiple of
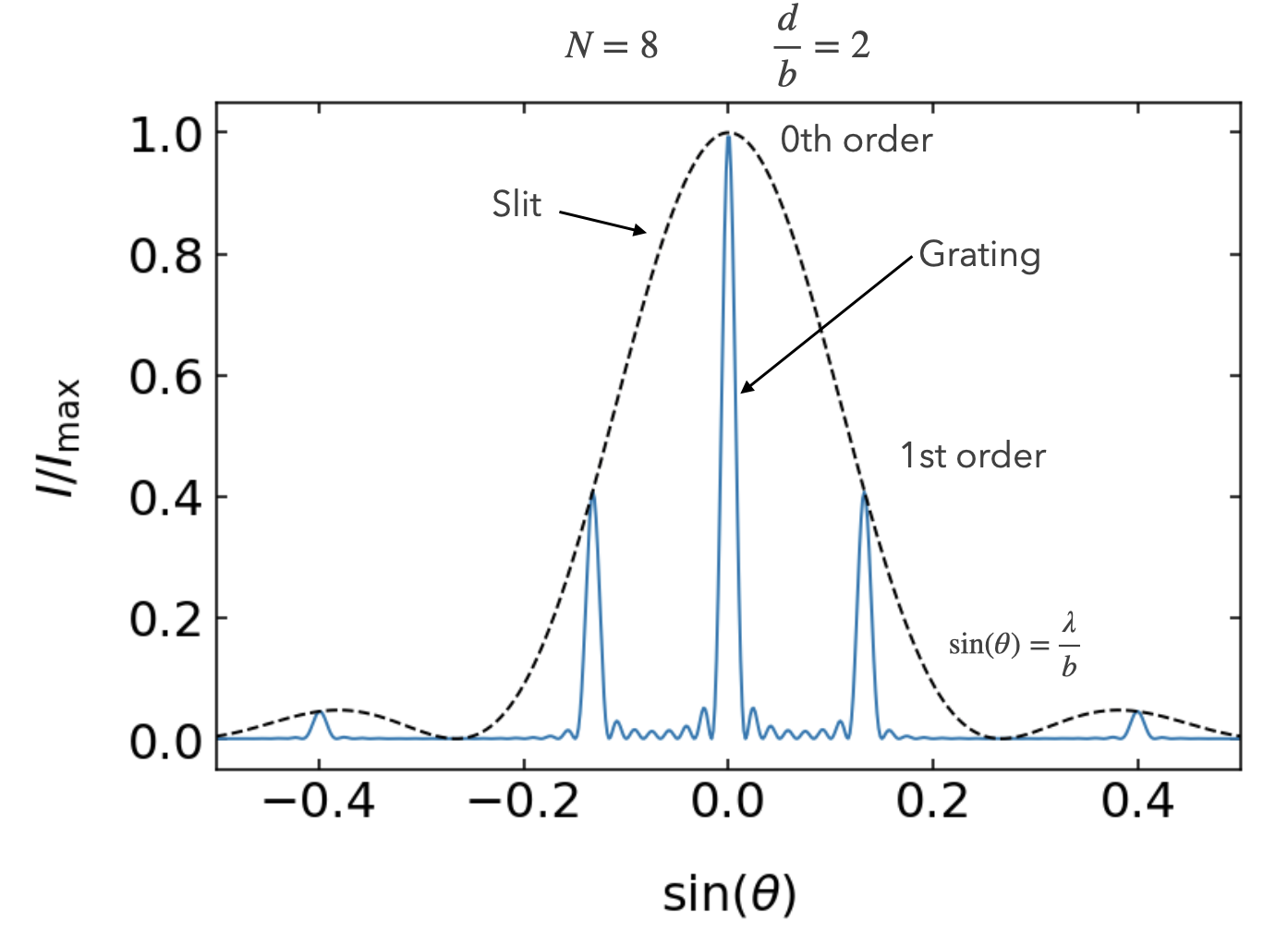
Fig.: Diffraction pattern of a grating wher 8 slits with a width of 2 µm and a distance of 4 micrometers are illuminated by a wavelength of 532 nm.
Influence of the Slit Width¶
The two plots below show the influence of the slit width while the slit distance is the same. We have again
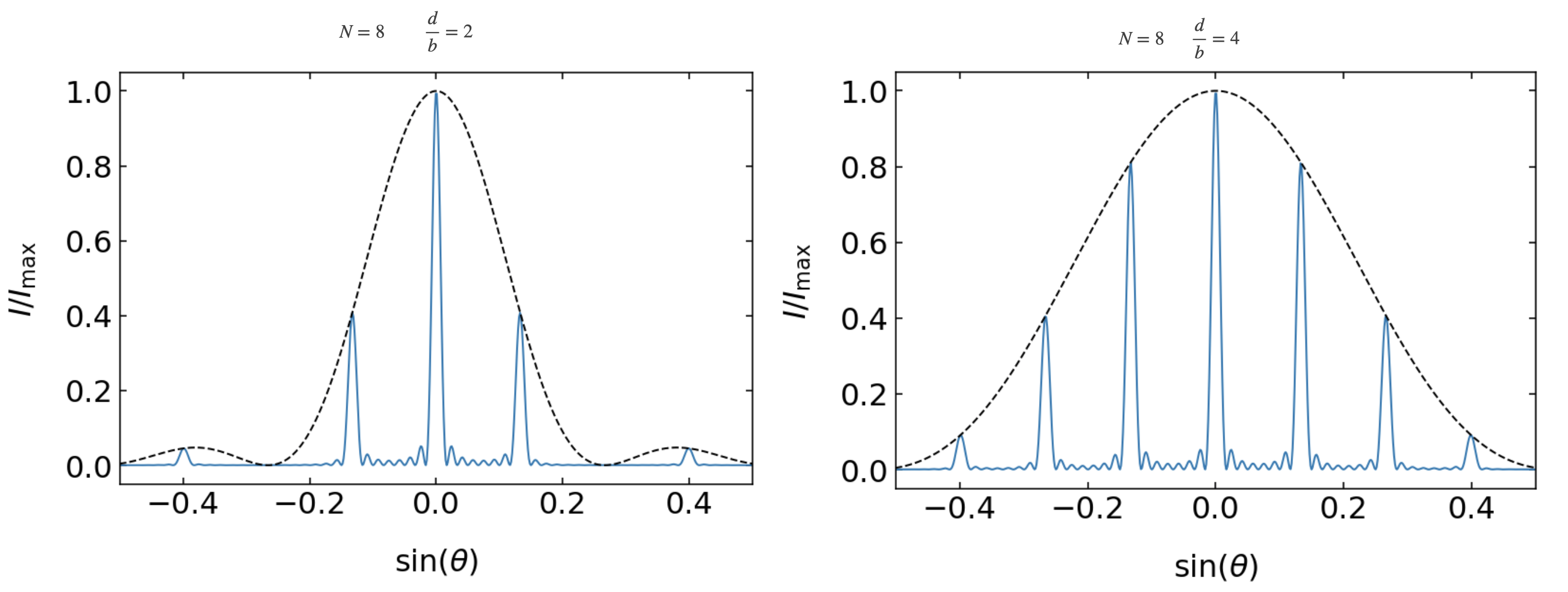
Fig.: (Left) Diffraction pattern of a grating with
Influence on the Slit Number¶
When using an increased slit number, we obtain the main diffraction peaks are becoming sharper. The location of the main peaks for the wavelength is unchanged, but as we have now
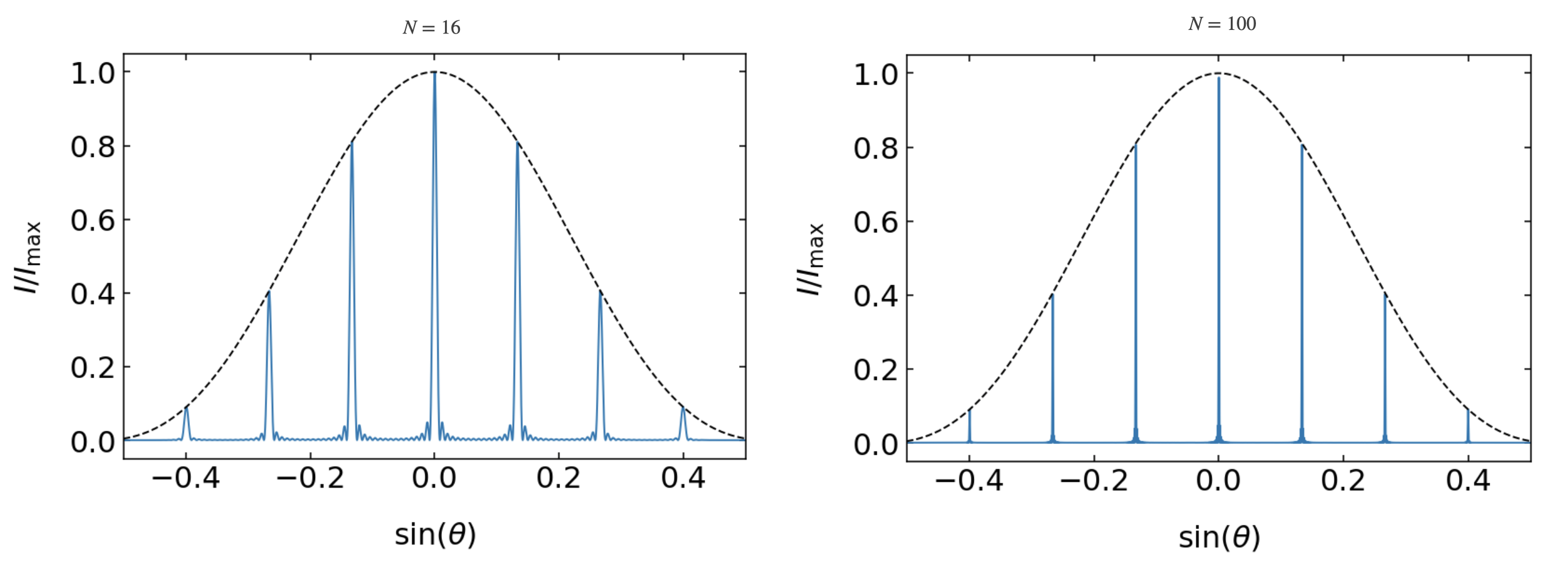
Fig.: (Left) Diffraction pattern of a grating with
Spectral resolution¶
For the spectral resolution we have to define a criterium again, that allows us to quantify the spectral resolution. We borrow the idea we used from the optical resolution of the microscope, i.e. that two peaks are separable, if the second peak is located at the minimum of the first diffraction pattern. Here the diffraction patterns refer not to different objects on space but to different wavelength
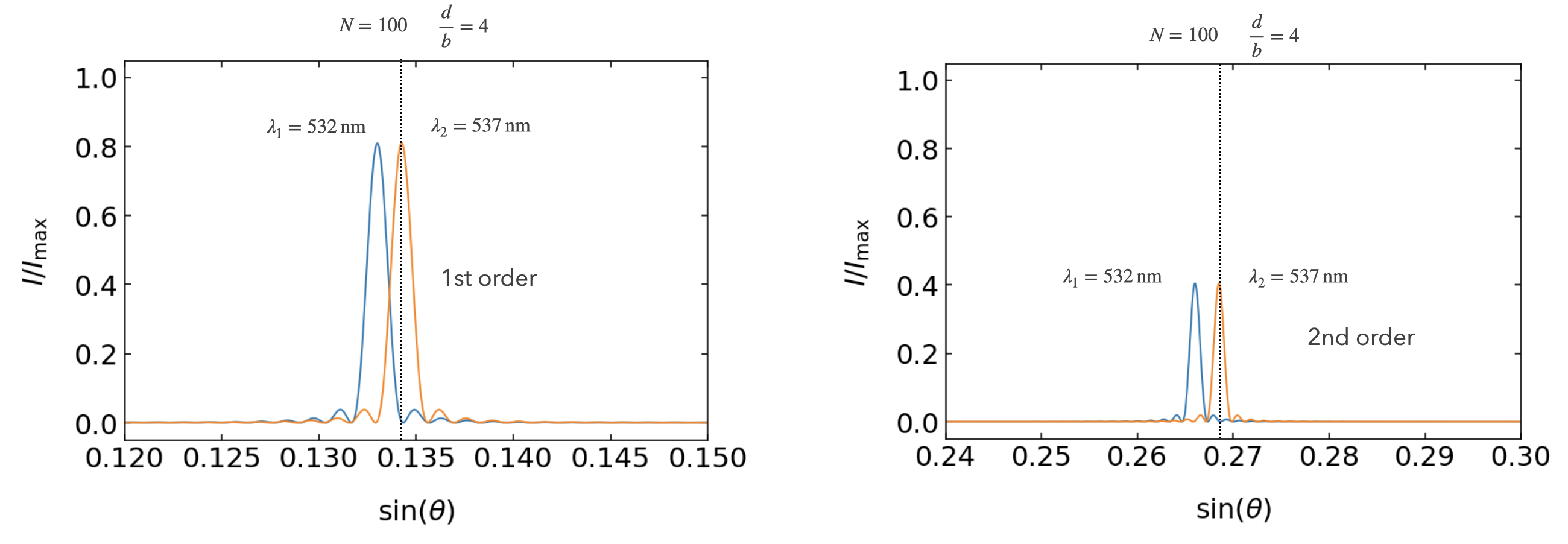
Fig.: Rayleigh resolution limit a grating with
Let us have a look at the
The next secondary minimum to larger angles of the diffraction pattern is then located at a position, where the numerator of the multiple wave interference
becomes zero or the argument
becomes a multiple
This angle has to correspond to the position of the main peak of the first order diffraction of the wavelength
Combining both equations for the two wavelength yields
and after some rearrangements (and setting \lambda_1=:nbsphinx-math:lambda)
This is the resolving power
Our finding is illustrated in the Figure above. Where we achieve a resolution of about 5 nm, when using


Fig.: Diffraction pattern observed for a grating in the lecture with red light (left) and white light (right).
